La frecuencia con la que los animales voladores, sean aves, insectos o murciélagos, agitan sus alas es proporcional a la raíz cuadrada de su masa corporal dividida por el área alar. Investigadores daneses han dado con esta fórmula, que también se puede aplicar para animales nadadores como las ballenas y los pingüinos.
La capacidad de volar ha evolucionado de forma independiente en distintos grupos de animales. Para minimizar la energía necesaria, los biólogos esperaban que hubiera un patrón en la frecuencia con la que las distintas especies baten las alas, pero encontrar una descripción matemática común a todas resultaba difícil.
Ahora, investigadores de la Universidad de Roskilde (Dinamarca) lo han conseguido. En la revista de acceso abierto PLOS ONE presentan una ecuación universal que describe la frecuencia del batido alar en aves, insectos y murciélagos, e incluso en animales nadadores como las ballenas, a pesar de su diferente tamaño, historia evolutiva y forma de sus estructuras alares o natatorias.
Una de las autoras, Tina Hecksher, explica a SINC la esencia de esta fórmula, derivada de principios físicos: “La frecuencia del batir de alas (f) es proporcional a la raíz cuadrada de la masa (m) del animal dividida por el área (A) del ala o aleta”. En la versión completa de la ecuación también se incluyen otros parámetros como la intensidad del campo gravitatorio y la densidad del aire.
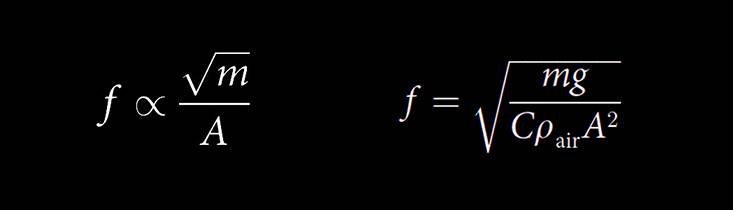
Versión simple de la ecuación universal (izquierda), donde la frecuencia (f) del batido alar es proporcional a la raíz cuadrada de la masa del animal dividida por el área del ala o aleta. A la derecha, la formula completa, donde también se incluye la intensidad del campo gravitatorio (g), un valor adimensional llamado C (que describe la forma, movimiento y otras características de las alas) y la densidad del aire (ρair). / Jensen et al./PLOS ONE
“Hemos descubierto que todos los animales voladores siguen esta proporcionalidad con aproximadamente el mismo coeficiente –subraya–. Además, con una extensión de esta fórmula a los animales nadadores se demuestra que siguen la misma relación universal (cuando se corrige la flotabilidad y la diferencia entre la densidad del aire y del agua). No hay ninguna fórmula más simple físicamente significativa que pueda describir la frecuencia del ‘aleteo’ en los animales voladores o nadadores”.
No hay ninguna fórmula más simple físicamente significativa que pueda describir la frecuencia del batir de alas o aletas en los animales voladores o nadadores
Los autores comprobaron la exactitud de su ecuación con los datos publicados sobre las frecuencias del batir de alas de abejas, polillas, libélulas, escarabajos, mosquitos, murciélagos y aves de distintos tamaños, desde colibríes hasta cisnes. También lo confirmaron con información sobre las frecuencias en el movimiento de aletas en pingüinos y varias especies de ballenas, como las jorobadas y las mulares del norte.
Los resultados de 414 animales, desde estos grandes cetáceos hasta los pequeños mosquitos, que difieren en casi un factor 10000 en la frecuencia de la agitación de las alas y las aletas, caen en la misma línea de la gráfica que han representado. “Como físicos, nos sorprendió ver lo bien que funciona nuestra sencilla predicción de la fórmula del batido de las alas para una colección tan diversa de animales”, apuntan los autores.
Por último, calcularon que un pterosaurio extinguido (Quetzalcoatlus northropi) –el mayor animal volador jamás conocido– pudo mover sus alas de 10 metros cuadrados a una frecuencia de 0,7 hercios o veces por segundo.
“La ecuación, junto a los datos empíricos, ofrece una receta para calcular la frecuencia del batido alar dada una masa y una superficie alar específicas”, destaca Hecksher, y aunque no está pensada para animales no voladores o nadadores pone el ejemplo de cómo se aplicaría en nuestra especie: “Si una persona pesa 70 kg y se construye unas alas con una superficie total de 2 m2, necesitaría batirlas unas 4 veces por segundo para mantenerse en el aire. Esto es muy difícil, ¡incluso sin las alas! Por nuestra propia experiencia al mover los brazos, podemos concluir que el ser humano no está hecho para volar, aunque la ecuación no lo descarta”.
Si un humano pesa 70 kg y se construye unas alas con una superficie de 2 m2, necesitaría batirlas unas 4 veces por segundo para mantenerse en el aire
El estudio demuestra que animales voladores tan distintos como las mariposas y los murciélagos, por ejemplo, han evolucionado hacia esta relación relativamente constante entre masa corporal, superficie alar y frecuencia del batido de alas o ‘aleteo’ (aunque este último término se aplica al movimiento de alas sin echar a volar, por lo que en este contexto es más correcto el primero).
Sobre los animales nadadores, los investigadores reconocen que no encontraron estudios con toda la información necesaria, por lo que unieron datos de varios para realizar las comparaciones y estimaciones.
En cualquier caso, con algunos ajustes, esta ‘receta’ también es válida para los animales buceadores con flotabilidad positiva que, como las ballenas y pingüinos, deben mover continuamente el agua hacia arriba con sus aletas para mantenerse sumergidos. Se excluyen a los peces, ya que estos ajustan su flotabilidad con una vejiga natatoria.
Según los autores, posibles animales extremadamente pequeños tampoco encajarían en la ecuación. “Predecimos que existe un límite determinado por la dinámica de fluidos. Para animales más pequeños que cualquier insecto medido hasta ahora derivamos otra ecuación, a saber, que la frecuencia del batir de alas es proporcional a la masa dividida por el área, es decir, sin raíz cuadrada. Será interesante investigarlo con nuevos estudios”, señala Hecksher, lo que podría tener implicaciones en el desarrollo de futuros nanobots voladores.
Referencia:
Jensen JH et al. “Universal wing- and fin-beat frequency scaling”. PLOS ONE, 2024
Ecuaciones para modelar el crecimiento de tumores, algoritmos para probar futuras máquinas, avanzadas teorías de computación y una fórmula para marcar un gol son algunos de los temas que se han tratado esta semana en la capital andaluza durante el 9º Congreso Europeo de Matemáticas.
La Academia Noruega de Ciencias y Letras ha concedido el considerado ‘Nobel de las matemáticas’ a este matemático francés “por sus contribuciones innovadoras a la teoría de la probabilidad y al análisis funcional, con aplicaciones excepcionales en física matemática y estadística”.
