La cooperación, el poder de los débiles

“Imagina tres o cuatro grupos de trabajo diferentes. Habrá uno de ellos más fuerte que los demás. Para crecer en importancia, los débiles solo tienen dos opciones: aliarse con el fuerte o cooperar entre sí. Las matemáticas nos dicen que la cooperación suele ser la mejor estrategia para los débiles y que, curiosamente, es también la más beneficiosa para el conjunto. Además, cualquiera de los débiles en solitario puede forzar esta situación. Un poder del que carecen los fuertes”.

Así explica Jacobo Aguirre, investigador del Centro Nacional de Biotecnología del CSIC (CNB-CSIC), su último trabajo publicado en la revista Nature Communications junto a Jaime Iranzo, de los Institutos Nacionales de Salud de EEUU y Javier M. Buldú de la Universidad Rey Juan Carlos y el Centro de Tecnología Biomédica (UPM).

El estudio se centra en entender las relaciones establecidas entre comunidades en forma de red que compiten por ganar importancia, lo que los investigadores denominan una red de redes. Los autores combinan en su estudio la teoría de juegos, conocida por los trabajos que concedieron el Nobel a John F. Nash; y la ciencia de redes complejas.

En este juego solamente existen dos soluciones estables: la cooperación o la sumisión. La primera es beneficiosa para los competidores débiles y la segunda es positiva para el más fuerte. Los resultados muestran claramente que la primera opción es, además, la mejor para el conjunto.

Pero lo más sorprendente es que cada una de las comunidades modestas es capaz de provocar una transición desde un sistema de sumisión al poderoso a uno de cooperación. “Cualquiera de los competidores débiles tiene el poder de inducir un cambio de estrategia global sin importar lo que haga el competidor fuerte, que es incapaz de cambiar la situación. Este es el gran poder de los indefensos. Tienen en sus manos el destino del conjunto”, explica Javier M. Buldú.

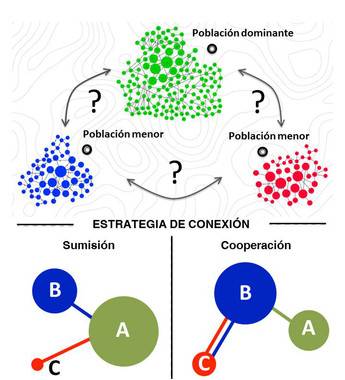
Estrategia de colaboración entre poblaciones de la India. / Jaime Iranzo, Javier M. Buldú and Jacobo Aguirre.

Según los autores, esta línea de trabajo nació cuando estudiaban procesos evolutivos en secuencias de ARN –un ácido que forma parte del material genético de los seres vivos–, pero la teoría es aplicable a multitud de juegos y situaciones en la vida real. Para realizar el estudio, los científicos han analizado ejemplos reales de economía, biología o relaciones sociales.

Microcréditos en la India

Como primer ejemplo, el trabajo analiza una red de interacciones entre tres pueblos del sur de la India en el contexto de un programa de microcréditos. El estudio muestra cómo las autoridades de una de las poblaciones más pequeñas deberían promover conexiones con las comunidades vecinas para minimizar los riesgos financieros asociados a plagas o fenómenos meteorológicos que pudieran afectar a las plantaciones de las que depende el pueblo.

El dilema surge a la hora de decidir con quién aliarse. Pueden optar por asociarse a la ciudad más importante de la región, un modelo en el cual la principal beneficiada sería esta última. La opción alternativa, es decir, la asociación entre las poblaciones débiles, les permitiría superar a la ciudad fuerte. “El resultado de nuestro trabajo habla claramente: esta es la mejor opción desde el punto de vista global”, explican los autores.

La investigación contra el ébola

Varios grupos de investigación de todo el mundo trabajan desvelando los misterios del virus del Ébola. Este ha sido el segundo ejemplo que los autores han destacado en su trabajo.

El estudio analiza las potenciales colaboraciones de los virólogos de la Universidad de Oxford con otros centros europeos. En este escenario, la universidad tendría que decidir qué estrategia le conviene más promover, es decir, con quién asociarse. “Creemos que la teoría que presentamos en nuestro trabajo puede ayudar a los centros de investigación a tomar la mejor decisión posible a la hora de buscar colaboraciones”, indican.

La conservación del oso pardo

Durante décadas, el esfuerzo de conservación del oso pardo en los Pirineos ha estado coordinado por España, Francia y Andorra. Cada país cuenta con sus propias zonas de reserva entre las que se establecen corredores ecológicos a través de los cuales los osos pueden pasar de una reserva a otra. Este es un buen ejemplo de que, en beneficio de una especie protegida, a menudo tres o más administraciones deben coordinarse para establecer vías de conexión entre sus respectivas zonas protegidas. El nuevo trabajo arroja luz acerca de la forma más eficiente de establecer dichos corredores, optimizando el movimiento y la recuperación de la especie.

En definitiva, según concluyen los autores en su trabajo, “la amplia aplicabilidad de este modelo, hace del ‘poder de los débiles’ un concepto a tener en cuenta a partir de ahora en la modelización de sistemas tecnológicos, biológicos y sociales”.