La guerra contra el COVID-19 se lucha en muchos frentes. Entre las armas que aportan las matemáticas destacan tres: el modelo SIR, que realiza predicciones como el previsible pico de contagios en España a principios de abril; el teorema de Bayes, que ayuda a actualizar la probabilidad de que se extienda COVID-19 con nuevos datos; y la teoría de juegos, que nos habla de sacrificar el beneficio individual por el bien común para vencer a este enemigo invisible.
Desde que el nuevo coronavirus SARS-Cov-2 salió de China y la enfermedad COVID-19 se ha extendido por el mundo, los países a los que ha llegado la pandemia han tomado medidas drásticas para aplanar sus curvas de infectados diarios, es decir, bajar y retrasar su pico lo máximo posible para que no colapsen los sistemas sanitarios.
Detrás de esas gráficas hay modelos matemáticos que recogen las características de los brotes epidémicos y permiten realizar predicciones. Sin duda uno de los más utilizados es el modelo SIR, cuyas siglas hacen referencia a las tres curvas o grupos de población implicados en una epidemia: los susceptibles (S) de contraer la enfermedad, los infectados (I) y los recuperados (R).
En algunas versiones los fallecidos se incluyen en R (aunque resulte irónico) para facilitar los cálculos, pero en la mayoría salen del sistema, ya que las personas pueden morir (también nacer y se puede considerar) estando en cualquiera de los tres grupos.
“La suma del número de susceptibles, recuperados, infectados y fallecidos es constante en cualquier instante de tiempo y es igual a la población inicial”, explica la matemática Anabel Forte de la Universidad de Valencia, quien destaca la flexibilidad de este modelo de ecuaciones diferenciales para entender cómo varía el número de personas en cada categoría, así como el esfuerzo actual para aplanar una de las curvas: la de infectados.
Otro matemático, Manuel de León, del Instituto de Ciencias Matemáticas (ICMAT) recuerda que SIR "es el modelo compartimental de Kermack-McKendrick, inspirado a su vez en el de Ronald Ross –que en 1911 modelizó la propagación de la malaria–. La idea del modelo compartimental es dividir la población en compartimentos y ver como se pasa de uno a otro, en este caso de S a I y luego a R".
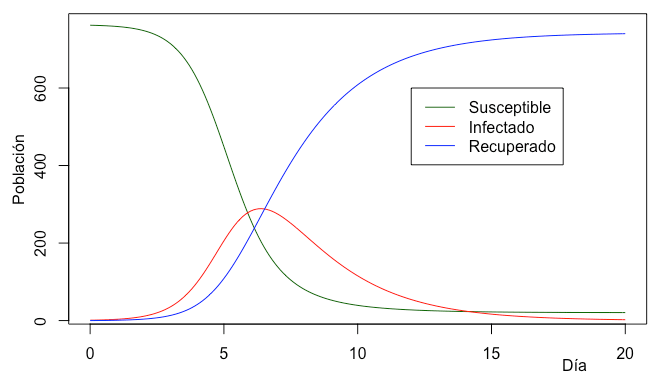
Ejemplo de las curvas de un modelo SIR (sin mortalidad). / Anabel Forte
“Una cuestión relevante es el valor de los parámetros que incluimos en las ecuaciones diferenciales, porque en una epidemia nueva como esta no los conocemos a priori y los vamos a ir estimando”, apunta De León, quien subraya la importancia de uno de los parámetros: R0, que indica el promedio de infecciones que causa un individuo contagiado.
“R0 se calcula a partir de los parámetros del modelo y puede cambiarse si modificamos nuestro comportamiento”, añade Forte, “y este número de personas a las que alguien infectado va a contagiar tiene que ver con la virulencia de la enfermedad y con el número de contactos que mantenemos”. De ahí la importancia de seguir las recomendaciones higiénicosanitarias y el aislamiento que piden las autoridades.
Dependiendo del R0, se puede aplanar la curva de infectados: “Lo ideal es que esté por debajo de 1 porque así, la epidemia irá desapareciendo por si sola –dice la matemática–. El R0 del coronavirus en circunstancias normales anda entre 1,5 y 2,5, que no es demasiado alto comparado con el del sarampión, por ejemplo, que está entre 14 y 15. Pero eso no significa que no sea peligroso. Solo hay que acordarse de que el de la gripe española fue de 2,1. Lo importante es reducirlo”.
Una de las extensiones del modelo SIR es SEIR, un sistema de ecuaciones donde se incorpora diferenciada la población expuesta (E), aquellas personas que incuban el virus sin mostrar síntomas. Un grupo de investigadores de universidades gallegas y de Portugal lo han utilizado para modelizar la evolución de la pandemia y ayudar en la toma de decisiones.
“Adaptandonos a las características propias de COVID-19, añadimos tres subpoblaciones (P de superpropagadores, A de infectados pero asintomáticos, H de hospitalizados) al modelo, con parámetros ajustados en función de los datos propios de este coronavirus desde que empezó en China”, explica uno de los autores, Juan José Nieto, de la Universidad de Santiago de Compostela.
“Mientras trabajábamos con el modelo, al hacerse público el 4 de marzo el primer positivo en Galicia, reparamos que el pico de la epidemia se produciría en torno a la primera semana de abril, hecho que pusimos en conocimiento de nuestras autoridades”, señala Nieto, y la predicción se puede extender a toda España: “Dado que ese máximo se puede alcanzar a los 20-35 días del primer caso, el pico se alcanzará previsiblemente a principios de abril”
Además de los modelos epidemiológicos, otras herramientas como las teorías y los teoremas matemáticos también tienen su aplicación en las predicciones y circunstancias que rodean a esta pandemia.
Un ejemplo es el teorema de Bayes, que describe la probabilidad de un suceso basándose en el conocimiento previo de las condiciones relacionadas con ese suceso. De León lo resume así: “La información acerca de un determinado fenómeno tras el análisis de los datos (distribución a posteriori), se obtiene actualizando los conocimientos previos (distribución a priori) con los nuevos datos (información que vamos obteniendo de las muestras)”.
El matemático ofrece un ejemplo teórico de lo que la estadística bayesiana puede aportar: "En determinados casos podemos deducir que vacunar a los niños es mejor solución que vacunar a toda la población, o a un segmento de la población por encima de una cierta edad, porque sean los mayores transmisores de esa enfermedad. De esta forma podemos ser más eficaces en combatir una epidemia".
“El teorema de Bayes es una herramienta estadística que nos puede ayudar a actualizar nuestro conocimiento sobre la probabilidad de que se extiendan enfermedades como COVID-19 a medida que se van teniendo nuevos datos”, apunta Forte.
La investigadora también destaca la importancia de las matemáticas para fomentar actitudes positivas de la gente frente a esta crisis sanitaria, como las enseñanzas de la teoría de juegos, muy utilizada en economía, informática y otros campos para estudiar cómo conseguir el mayor beneficio en situaciones de competitividad.
Uno de los problemas clásicos de esta teoría es el dilema del prisionero, que en principio muestra que dos individuos podrían no cooperar, aunque parezca que lo mejor para ambos sea hacerlo. Pero el dilema se puede plantear de diversas formas y en distintos escenarios, con ganancias mayores o menores para los participantes.
Considerando, por ejemplo, si se deben aislar dos individuos asintomáticos contagiados por el coronavirus, la opción en la que ganamos todos es que ambos lo hagan, no uno solo, como recoge en Twitter la matemática Clara Grima de la Universidad de Sevilla.
Dilema del prisionero aplicado a una situación donde dos personas, A y B están contagiados pero no presentan síntomas. / Clara Grima
La teoría de juegos se ha ido incorporando a los modelos para tener en cuenta el comportamiento social de los individuos, apunta De León, quien plantea preguntas relacionadas con COVID-19: “¿Somos obedientes a las instrucciones que nos dan a fin de reducir los contactos y las transmisiones?, ¿nos lavamos las manos como nos aconsejan?, ¿cómo influye la comunicación desde las autoridades y los medios de comunicación en nuestro comportamiento? Pasa como en teoría de juegos: si me comporto bien, tendré menos opciones de contagiarme”.
Por su parte, Forte concluye: “Yo creo que la teoría de juegos aquí nos habla de la solidaridad en varios sentidos. Aunque a ti personalmente te fastidie, si todos nos quedamos en casa ayudamos a reducir el R0 y, por tanto, al bien común. Pero también tiene que ver con las compras en los supermercados. Si todos vamos como locos a llenar las despensas, habrá gente que lo pase mal y no tenga que comer. Se trata de reducir el beneficio individual en pos del bien común”.
Ecuaciones para modelar el crecimiento de tumores, algoritmos para probar futuras máquinas, avanzadas teorías de computación y una fórmula para marcar un gol son algunos de los temas que se han tratado esta semana en la capital andaluza durante el 9º Congreso Europeo de Matemáticas.
La frecuencia con la que los animales voladores, sean aves, insectos o murciélagos, agitan sus alas es proporcional a la raíz cuadrada de su masa corporal dividida por el área alar. Investigadores daneses han dado con esta fórmula, que también se puede aplicar para animales nadadores como las ballenas y los pingüinos.
